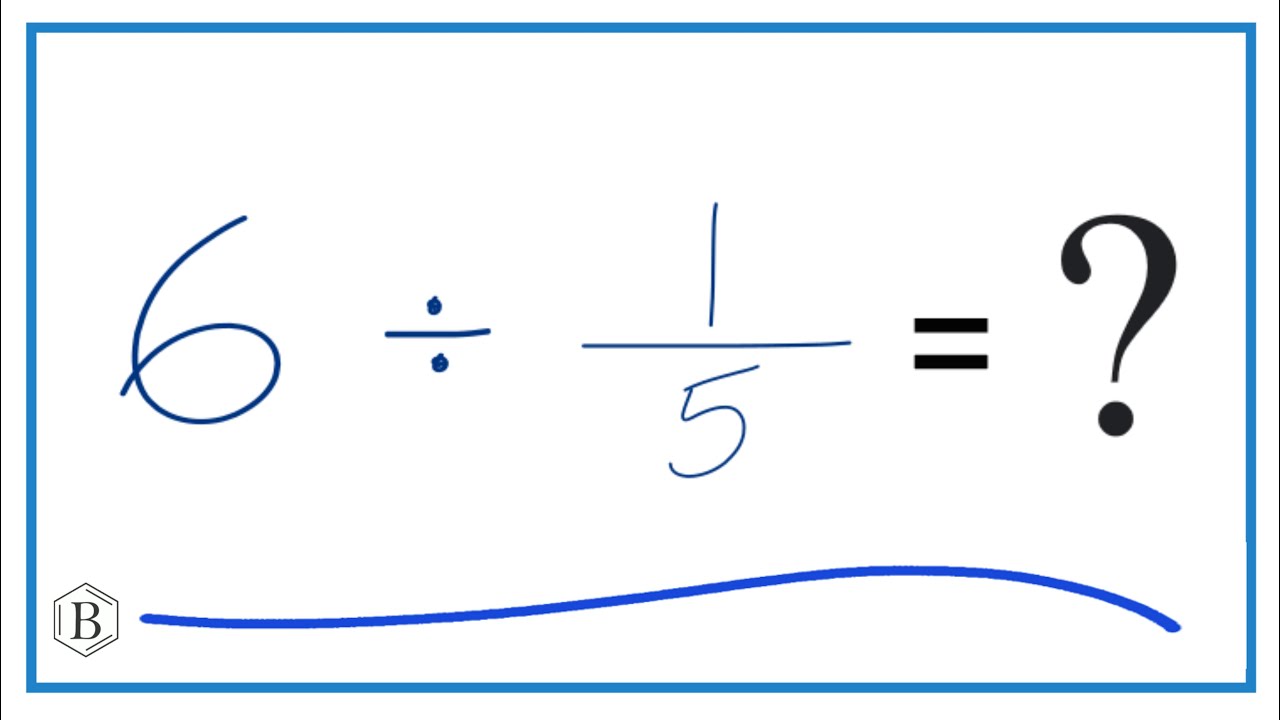Mastering Math Basics: The Significance Of 6 Divided By -3

Mathematics forms the foundation of countless aspects of our daily lives, from simple tasks like shopping to complex engineering feats. A fundamental concept within this vast subject is division, a process that helps us understand how numbers can be evenly distributed or divided into parts. Among the myriad of division problems one might encounter, "6 divided by -3" often serves as an intriguing example, especially for those beginning their journey into the world of negative numbers and integers. Understanding this calculation is not merely about arriving at a numerical answer; it opens the door to a deeper comprehension of mathematical principles and the behavior of numbers.

In a world where math is essential for academic and professional success, grasping core concepts such as division is vital. The problem "6 divided by -3" is more than a simple arithmetic exercise—it is a lesson in the rules governing positive and negative numbers. By mastering this calculation, learners gain insights into the properties of numbers, which are crucial for solving more complex mathematical problems. This knowledge is not only valuable in academic settings but also enhances everyday problem-solving skills, fostering logical reasoning and analytical thinking.

Moreover, as educational curriculums evolve to meet the demands of a rapidly changing world, it becomes increasingly important for students to have a solid understanding of basic mathematical operations. The simplicity of "6 divided by -3" makes it an excellent teaching tool, allowing educators to introduce essential concepts without overwhelming students. By exploring this division problem, learners can develop a robust mathematical foundation, preparing them for advanced studies and real-world applications where mathematical literacy is indispensable.

Table of Contents

• Understanding Division
• The Concept of Negative Numbers
• Mathematical Operations with Negative Numbers
• Solving 6 Divided by -3
• Real-World Applications of Negative Division
• Common Mistakes and Misconceptions
• The Importance of Order of Operations
• Historical Perspective on Negative Numbers
• Educational Strategies for Teaching Division
• Technological Tools for Learning Math
• The Role of Math in Critical Thinking
• Cross-Disciplinary Connections with Math
• Frequently Asked Questions
• Conclusion

Understanding Division

Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It involves splitting a number (the dividend) into equal parts or groups, with the size of each part determined by another number (the divisor). The result of this operation is known as the quotient. In the context of "6 divided by -3," the number 6 represents the dividend, -3 is the divisor, and the quotient is the result we're seeking.

To truly grasp division, one must first understand its relationship with multiplication. Division can be thought of as the inverse operation of multiplication. For instance, if multiplying 2 by 3 gives us 6, then dividing 6 by 3 should return us to 2. This inverse relationship is crucial for solving division problems and verifying solutions.

Moreover, division is not always straightforward. Unlike multiplication, where the product of two numbers is always a single, definite number, division can result in whole numbers, fractions, or even undefined values if the divisor is zero. Therefore, understanding the nuances of division is essential for accurate calculations and problem-solving.

The Concept of Negative Numbers

Negative numbers, those less than zero, are a fundamental part of mathematics, though they can initially be challenging to comprehend. They are used to represent values below a certain reference point, such as temperatures below freezing or financial losses. The introduction of negative numbers significantly expanded the mathematical landscape, allowing for more comprehensive modeling of real-world phenomena.

Negative numbers possess certain properties that dictate how they interact with other numbers in mathematical operations. A key rule to remember is that multiplying or dividing two negative numbers results in a positive number, whereas multiplying or dividing a positive number by a negative number yields a negative result. This rule is essential for correctly solving problems involving negative numbers, such as "6 divided by -3."

To illustrate, consider the number line, where positive numbers extend to the right of zero and negative numbers to the left. Operations involving negative numbers can be visualized as movements along this line, with division leading to movements in the opposite direction of the divisor's sign.

Mathematical Operations with Negative Numbers

When performing mathematical operations with negative numbers, it's crucial to apply specific rules to ensure accuracy. These rules stem from the properties of negative numbers and their relationships with positive numbers. Understanding these rules is vital for correctly executing operations like addition, subtraction, multiplication, and division involving negative numbers.

For addition and subtraction, negative numbers can be treated as movements in opposite directions on the number line. Adding a negative number is akin to moving left, while subtracting a negative number is equivalent to moving right. This conceptualization helps demystify operations that would otherwise seem counterintuitive.

In multiplication and division, the sign of the result depends on the signs of the numbers involved. As mentioned earlier, the product or quotient of two numbers with like signs (both positive or both negative) is positive, whereas the product or quotient of numbers with unlike signs is negative. This rule is crucial for solving problems involving negative numbers, such as "6 divided by -3," ensuring that the correct sign is assigned to the quotient.

Solving 6 Divided by -3

To solve the division problem "6 divided by -3," we must apply the rules of division and the properties of negative numbers. As with any division problem, we begin by identifying the dividend and divisor. Here, 6 is the dividend, and -3 is the divisor.

The next step is to divide the numbers as if they were both positive, disregarding the signs momentarily. Dividing 6 by 3 yields 2, which is the absolute value of the quotient. However, we must consider the signs of the original numbers to determine the correct sign of the quotient.

Since the dividend (6) is positive and the divisor (-3) is negative, the quotient will be negative, following the rule that the quotient of numbers with unlike signs is negative. Thus, the solution to "6 divided by -3" is -2.

This solution not only demonstrates the application of division and negative number rules but also highlights the importance of understanding mathematical operations conceptually. By grasping these principles, learners can confidently tackle similar problems and develop a robust mathematical foundation.

Real-World Applications of Negative Division

Division involving negative numbers is not just an abstract mathematical concept; it has numerous practical applications in various fields. Understanding how to work with negative divisions is essential for solving real-world problems that involve deficits, reversals, or oppositional forces.

For instance, in finance, negative division can be used to calculate losses or debts. If a company experiences a loss of $6 over three months, dividing this loss by the three-month period results in a negative quotient, indicating a consistent monthly deficit.

Similarly, in physics, negative division can describe phenomena such as velocity or force in opposite directions. When a force of -6 Newtons is applied over a distance of 3 meters, the resulting negative acceleration can be understood through division, providing insights into the system's dynamics.

These applications underscore the practical value of mastering negative division, as it enables professionals to model and solve complex problems accurately. By understanding the principles behind "6 divided by -3," individuals can enhance their analytical skills and apply mathematical reasoning to diverse scenarios.

Common Mistakes and Misconceptions

While division is a fundamental mathematical operation, it is not immune to misunderstandings and errors, especially when negative numbers are involved. Recognizing and addressing these common mistakes is crucial for accurate problem-solving and mathematical proficiency.

One frequent error is neglecting the sign of the quotient. When dividing positive and negative numbers, it's essential to apply the rule that dictates the sign of the result. Failing to do so can lead to incorrect answers and misconceptions about the properties of numbers.

Another common mistake is confusing division with subtraction. While both operations involve numbers being reduced, their processes and outcomes are distinct. Division involves distributing a number into equal parts, while subtraction involves removing a specific amount from a number. Understanding this distinction is vital for correctly solving division problems.

Additionally, some learners may struggle with the concept of negative numbers, leading to errors in operations involving these values. To overcome these challenges, educators and learners alike should focus on building a strong conceptual foundation, emphasizing the rules and properties of negative numbers through visual aids and practical examples.

The Importance of Order of Operations

The order of operations is a fundamental principle in mathematics, ensuring that calculations are performed consistently and accurately. This principle, often remembered through the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction), dictates the sequence in which mathematical operations should be executed.

In the context of division, understanding the order of operations is crucial for solving problems correctly. When an expression contains multiple operations, division should be performed alongside multiplication, following any calculations involving parentheses and exponents.

For example, in the expression 6 / -3 + 2, division is performed before addition, resulting in a quotient of -2, which is then added to 2 for a final result of 0. Ignoring the order of operations would lead to an incorrect outcome, highlighting the importance of following this principle.

By adhering to the order of operations, learners can ensure the accuracy of their calculations, avoiding potential pitfalls and misunderstandings. This foundational knowledge is essential for tackling more complex mathematical problems and developing a strong mathematical skill set.

Historical Perspective on Negative Numbers

The concept of negative numbers has a rich and fascinating history, dating back to ancient civilizations. While the use of negative numbers is now commonplace, their acceptance and understanding took centuries to develop, reflecting the evolving nature of mathematical thought.

Early mathematicians, such as the ancient Greeks, struggled with the notion of numbers less than zero, as they did not fit within the existing framework of mathematics. It was not until the work of Indian mathematicians, such as Brahmagupta in the 7th century, that negative numbers began to gain recognition as legitimate mathematical entities.

Brahmagupta's groundbreaking work laid the foundation for the rules governing negative numbers, including the principles of addition, subtraction, multiplication, and division involving negative values. His contributions paved the way for further advancements by Islamic and European mathematicians, ultimately leading to the widespread acceptance of negative numbers in the mathematical community.

This historical perspective highlights the dynamic nature of mathematics as a discipline, continually evolving to accommodate new ideas and discoveries. Understanding the history of negative numbers enriches our appreciation of their significance and underscores the importance of mathematical exploration and innovation.

Educational Strategies for Teaching Division

Effective teaching strategies are essential for fostering a deep understanding of division, particularly when negative numbers are involved. Educators must employ diverse approaches to engage learners and facilitate the development of mathematical skills and confidence.

One effective strategy is the use of visual aids, such as number lines and diagrams, to illustrate the concept of division and the interaction between positive and negative numbers. These tools can help demystify abstract concepts, making them more accessible to learners.

Additionally, incorporating real-world examples and applications can enhance students' understanding of division and its relevance. By connecting mathematical concepts to everyday scenarios, educators can help learners see the practical value of their studies, fostering motivation and engagement.

Collaborative learning and hands-on activities can also be valuable tools for teaching division. Group work and interactive exercises encourage students to explore mathematical concepts through discussion and experimentation, promoting deeper understanding and retention.

By employing these strategies, educators can create a supportive and dynamic learning environment that empowers students to master division and other mathematical operations, preparing them for future success.

Technological Tools for Learning Math

In today's digital age, technological tools offer valuable resources for enhancing math education and supporting learners in their studies. From online tutorials and interactive apps to sophisticated software, technology provides diverse opportunities for exploring mathematical concepts and improving skills.

Online platforms, such as Khan Academy and Coursera, offer comprehensive courses and resources covering a wide range of mathematical topics, including division and negative numbers. These platforms provide learners with flexible, on-demand access to high-quality educational materials, enabling self-paced learning and skill development.

Interactive math apps, such as Photomath and Mathway, offer real-time problem-solving assistance, guiding users through calculations and providing instant feedback. These tools can be particularly helpful for learners who need additional support or practice outside the classroom.

Advanced software, like MATLAB and GeoGebra, allows students to explore complex mathematical concepts and visualize data, fostering a deeper understanding of mathematical principles. By integrating technology into math education, learners can access diverse resources that support their studies and enhance their mathematical proficiency.

The Role of Math in Critical Thinking

Mathematics plays a crucial role in developing critical thinking skills, which are essential for success in both academic and professional settings. By engaging in mathematical problem-solving, learners cultivate the ability to analyze information, evaluate options, and make reasoned decisions.

Through the study of division and other mathematical operations, students learn to approach problems methodically, breaking them down into manageable components and identifying patterns and relationships. This analytical approach fosters logical reasoning and enhances problem-solving abilities.

Moreover, math encourages creativity and innovation, challenging learners to explore multiple solutions and think outside the box. By experimenting with different approaches and techniques, students develop a flexible mindset that supports adaptability and resourcefulness.

Ultimately, the skills gained through the study of mathematics extend beyond the classroom, equipping individuals with the tools needed to navigate a complex and rapidly changing world. By fostering critical thinking, math education empowers learners to tackle challenges with confidence and make informed decisions in their personal and professional lives.

Cross-Disciplinary Connections with Math

Mathematics is not an isolated discipline; it intersects with numerous fields, enriching our understanding of the world and enabling innovative solutions to complex challenges. By exploring the connections between math and other subjects, learners can appreciate the interdisciplinary nature of knowledge and its applications.

In science, math is an indispensable tool for modeling phenomena, analyzing data, and conducting experiments. Whether it's calculating forces in physics, analyzing chemical reactions, or modeling biological processes, math provides the language and framework for scientific inquiry and discovery.

In engineering, math is fundamental to designing and optimizing systems, structures, and technologies. From calculating load distributions in civil engineering to analyzing circuit behavior in electrical engineering, math supports the development of innovative solutions and advancements in technology.

Math also plays a vital role in the arts, offering insights into patterns, symmetry, and proportions. Artists and designers often rely on mathematical concepts to create visually appealing compositions, while musicians explore mathematical relationships in rhythm, harmony, and acoustics.

By recognizing the cross-disciplinary connections between math and other fields, learners can develop a holistic understanding of knowledge and its applications, fostering creativity, collaboration, and innovation in their studies and future careers.

Frequently Asked Questions

1. Why is the result of 6 divided by -3 a negative number?

The result is negative because division follows the sign rules of multiplication. When dividing a positive number by a negative number, the quotient is negative, according to the rule that dictates the product or quotient of numbers with unlike signs is negative.

2. Can division by a negative number result in a positive quotient?

Yes, division by a negative number can result in a positive quotient if both the dividend and the divisor are negative, as the product or quotient of two numbers with like signs (both negative) is positive.

3. How can negative numbers be represented on a number line?

On a number line, negative numbers are positioned to the left of zero, extending infinitely. They represent values less than zero and can be visualized as movements opposite to positive numbers.

4. What are some real-world scenarios involving negative division?

Real-world scenarios involving negative division include calculating financial losses, modeling reversal forces in physics, and analyzing temperatures below a reference point. These applications demonstrate the practical value of understanding division with negative numbers.

5. How can educators effectively teach division involving negative numbers?

Educators can effectively teach division involving negative numbers by using visual aids, real-world examples, collaborative learning, and interactive activities. These strategies help learners grasp abstract concepts and apply them confidently.

6. What technological tools are available for learning math?

Technological tools for learning math include online platforms like Khan Academy, interactive apps like Photomath, and advanced software like MATLAB. These resources offer diverse opportunities for exploring mathematical concepts and improving skills.

Conclusion

The division problem "6 divided by -3" serves as a gateway to understanding fundamental mathematical principles and the behavior of numbers. By exploring this calculation, learners gain insights into the rules governing positive and negative numbers, developing a robust mathematical foundation that supports their academic and professional success.

Moreover, this exploration highlights the practical applications of negative division in various fields, from finance and physics to engineering and the arts. By recognizing the interdisciplinary nature of mathematics, learners can appreciate its relevance and significance in solving real-world problems and driving innovation.

Ultimately, mastering the concept of "6 divided by -3" and other mathematical operations equips individuals with the critical thinking and problem-solving skills needed to navigate a complex and rapidly changing world. Through effective education and the integration of technology, learners can develop the mathematical literacy essential for lifelong learning and success.